
Trading any financial market is a game of probabilities and NOT certainties. Even the smartest mathematicians understand this one fact that seems to allude struggling traders. Fortunately, the probabilities of trading are simple to understand. The best and most used likeness for comprehending probabilities in trading is the coin toss. The coin toss and the financial markets share one key common element: dual outcomes. At any given instant, the price can only travel in two directions, up or down. In a coin toss, no matter how many times you flip the coin, it will either land on heads or tails.
The next question becomes if we were to bet, for example, $10 that the coin will land on heads on every occasion, how long would we still have enough ‘betting money’ until the coin eventually lands on heads. In a nutshell, the same principle of money management in trading applies– you need to have enough money to keep ‘flipping the coin’ until it lands on heads.
The reality is that even though there is mathematically a 50% chance of either outcome, we cannot know with firm conviction exactly when it will land on heads. It could be after the first or the 20th flip. We could have a winning streak where it lands on heads six times or a losing streak where it lands on tails six times consecutively. The permutations are random. This analogy is probably the best approach to thinking about the probabilities here and is the complex reality of trading we need to face.
Probabilities of losing streaks
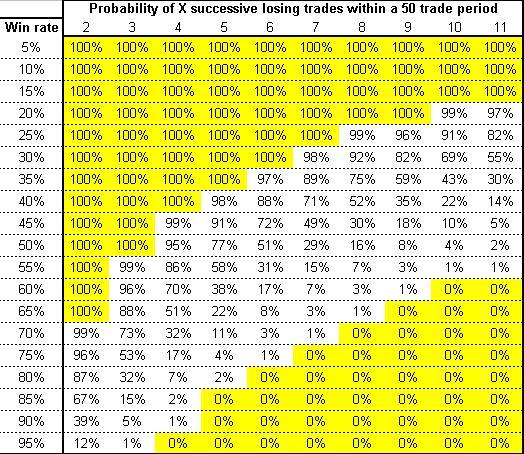
Probabilities matter more in managing losing streaks than in any other area. Losses are often undervalued even by the most confident traders. It’s natural to assume with a high amount of confidence that a trade is a sure winner without much thought that perhaps the next two or three in a row can lose.
The above image is a typical mathematical model that traders can use to understand better the likelihood of a losing streak over 50 trades. We must bear in mind that a losing streak can happen at any stage and no matter the trade frequency. Even for a trader that may trade twice a month, the probabilities of a losing streak are possible, albeit they would happen over a very long period,
How recency bias negatively affects traders
There are many interesting psychological battles that traders face in the markets. One prevalent psychological occurrence is recency bias. This type of bias defines a situation where the human mind favors recent events and assumes they will play out to an identical or similar degree in the future. For example, it’s pervasive to believe that a winning trade that traveled a substantial 200 pips will also occur on the next one. Since this is a recent event, the brain will almost trick the trader into acting in the same manner as they did recently,
However, in reality, due to the market’s randomness, that event has a 50-50 probability of occurring as established. In fact, the likelihood is the trader may lose the next trade or that the market may not travel 200 pips. The certainty of any trade is unpredictable, and each outcome is independent of the future one. Many psychological scholars assert that, cognitively, we tend to estimate the probability of something happening less on a long-term basis, but more on whatever occurred recently.
Why you must understand the law of large numbers
This law is the perfect explanation between winning percentages and probabilities. The law of large numbers dictates as the sample size of a series of outcomes expands, the closer it gets to its average. We can define the average outcome in the context of any financial market at 50%. Again, the perfect example used to understand probabilities here is a coin toss due to the identical results.

The above image demonstrates a simulated random coin toss performed 2000 times. If we bet on heads every time, there is a chance that the coin could land on heads in ten successions. However, this event wouldn’t mean the probability of the coin landing on heads overall is 100%. Regardless of how we start, we will get very close to 50% probability over any random number of coin tosses over an extended period. The same analogy applies exactly to trading.
The law of large numbers stresses the importance that trading is a very long game based on a large sample size of trades. In that sample size, there is a random distribution of winners and losers. Trading the markets is almost like a continuum instead of a defined destination. Essentially, long-term gains and performance should be more sought-after the opposite. The latter is very challenging to achieve consistently due to the nature of volatile markets.
Why winning percentages don’t matter
Most traders tend to fixate on the winning percentage to assert how good a trading strategy is while ignoring that the winning percentage says nothing about the probability of a winning trade. In essence, winning percentages don’t matter as we’ve established that 50-50 is the realistic probability ratio. A point of intrigue is that the winning percentage may show lower or higher than 50% over a large sample size, though overall, the trading account itself has gained substantially.
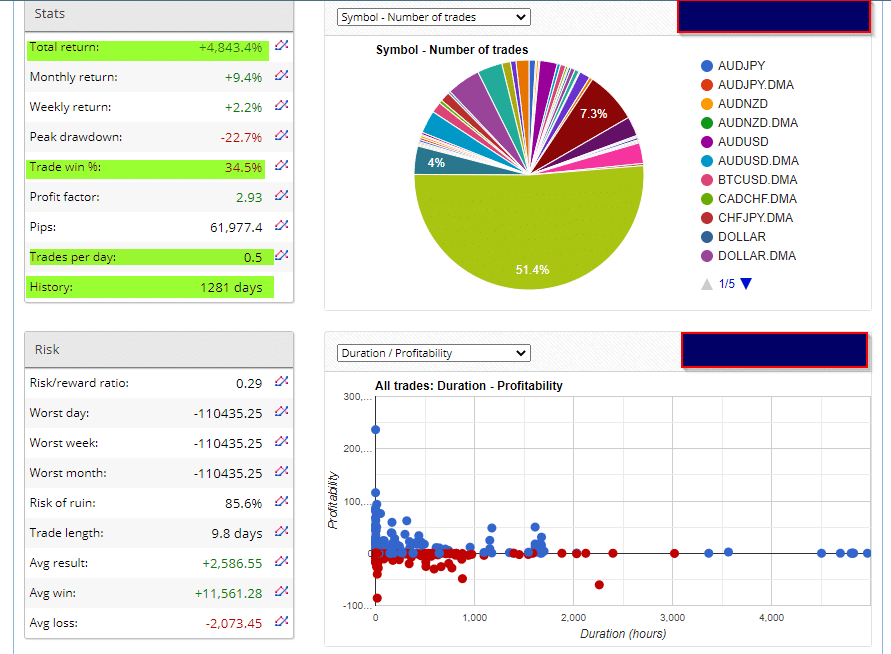
The account statement above emphasizes many of the concepts of the law of large numbers and probabilities. Firstly, we should observe that the trade win percentage is 34.5%, surprisingly lower than 50%. So, granted, if this trader continued trading, over weeks, months, or even years, that percentage would get close to 50%. Though even at 34.5%, an uneducated trader may assume that to be a low win percentage. In the long run, this account returned a whopping gain close to 5000% over approximately three and a half years (1281 days).
Another vital point to note is the average amount of trades is 0.5. If we multiply that by the number of days the account was live (1281 days), we could approximate that the trader made 640 trades over that period.
Conclusion
All these components in all the observed images suggest why winning percentages are irrelevant when we thoroughly comprehend probabilities as they should. It also stresses the importance of consistency, observing your performance over the long run, and the power of risk to reward.








Leave a Reply